2 posts tagged with "metal"

Thanks to Alex Kuzmin, Andy Guzman, Miha Stopar, Sinu, and Zoey for their generous feedback and review.

TL;DR​

• The Problem: Delegating ZK proof generation to servers often fails to preserve privacy, as the server sees your private inputs, though there are recent researches on private proof delegation ^{1 2 3} to mitigate this issue. Ultimately, true privacy requires client-side proving, but current performance is too slow for mainstream adoption.
• The Opportunity: Modern mobile phones and laptops contain GPUs well-suited to accelerating parallelizable ZK primitives (NTT, MSM, hashing). Benchmarks show field operations on smaller fields like M31 achieve more than 100x throughput compared to BN254 on an Apple M3 chip ⁴.
• The Gap: No standard cryptographic library exists for client-side GPU implementations. Projects reinvent primitives from scratch, and best practices for mobile-specific constraints (hybrid CPU-GPU coordination, thermal management) remain unexplored.
• Post-Quantum Alignment: Smaller-field operations in post-quantum (PQ) schemes (hash-based, lattice-based) map naturally to GPU 32-bit ALUs, making this exploration more valuable as the ecosystem prepares for quantum threats.

1. Privacy is Hygiene​

Ethereum's public ledger ensures transparency, but it comes at a steep cost: every transaction is permanently visible, exposing users' financial histories, preferences, and behaviors. Chain analysis tools can easily link pseudonymous addresses to real-world identities, potentially turning the blockchain into a surveillance machine.

As Vitalik put it, "Privacy is not a feature, but hygiene." It is a fundamental requirement for a safe decentralized system that people are willing to adopt for everyday use.

Delegating ZK proof generation to servers undermines this hygiene. While server-side proving is fast and convenient, it requires sharing raw inputs with third parties. Imagine handing your bank statement to a stranger to "anonymize" it for you. If a server sees your IP or, even worse, your transaction details, privacy is compromised regardless of the proof's validity. Though recent studies explore private delegation of provers ¹, true sovereignty requires client-side proving: users generate proofs on their own devices, keeping data private from the start.

This is especially critical for everyday Ethereum privacy. Think of sending payments, voting in DAOs, or managing identity-related credentials (e.g. health records) without fear of exposure. Without client-side capabilities, privacy-preserving tech remains niche, adopted only by privacy-maximalist geeks. Hence, accelerating proofs on consumer hardware could be the bedrock for creating mass adoption of privacy, making it as seamless as signing a transaction today.

2. GPU Acceleration: A Multi-Phase Necessity for Client Proving​

Committing resources to client-side GPU acceleration for ZKP is both a short-term and long-term opportunity for Ethereum's privacy landscape. GPUs excel at parallel computations, aligning perfectly with core primitives that could be used in privacy-preserving techs like ZKP and FHE, and client devices (phones, laptops) increasingly feature growing GPU capabilities. This could reduce proving times to interactive levels, fostering mass adoption.

Current Status and Progress​

Although client-side proving is a reality, the user experience is still catching up. CSP benchmarks from ethproofs.org show that while consumer devices can now generate proofs in seconds, the process often takes longer than 100ms. For scenarios requiring real-time experience, like payments or some DeFi applications, this delay creates noticeable friction that hinders adoption.

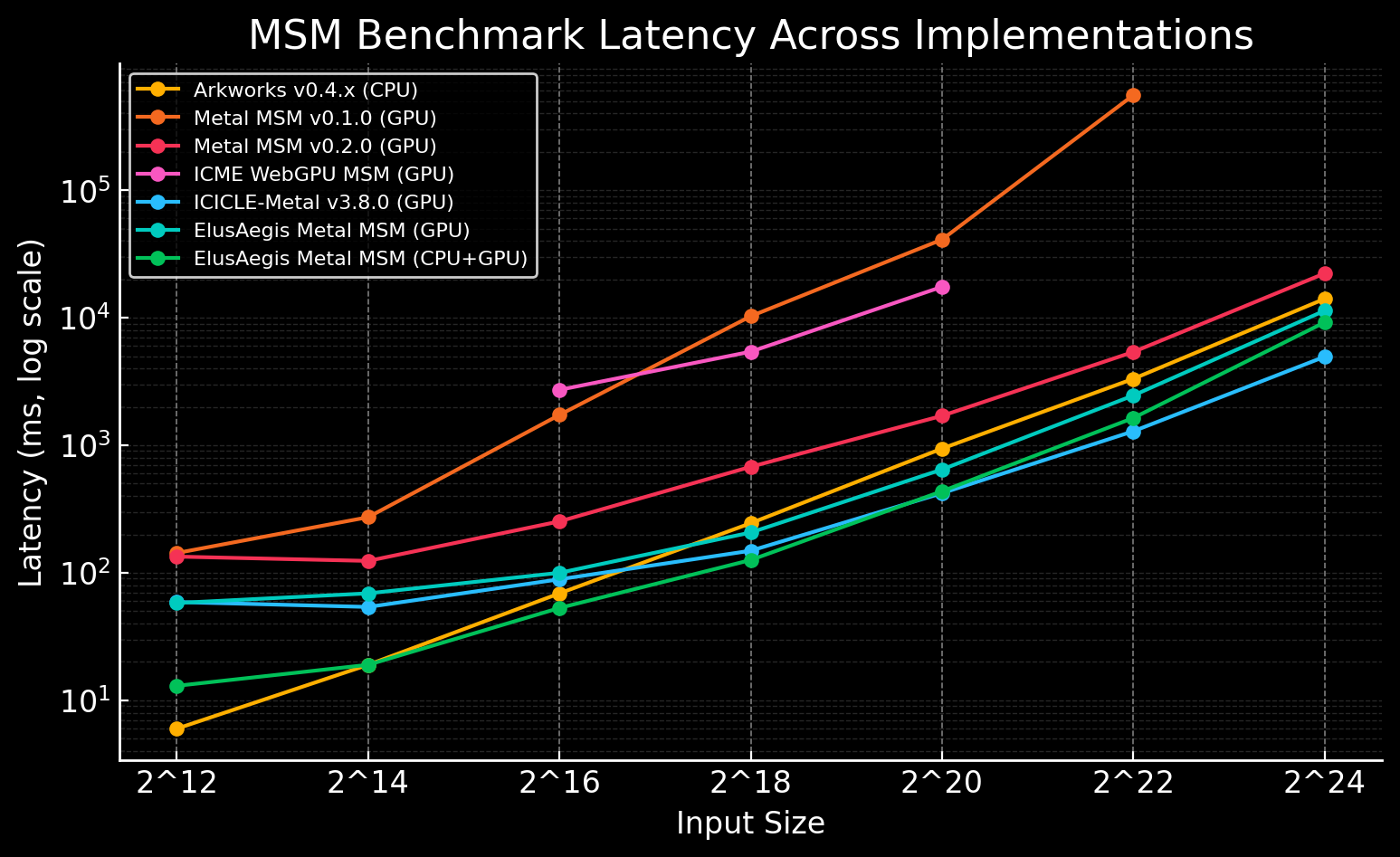
CSP benchmarks from ethproofs.org 5. Snapshot taken on January 19, 2026

Several zkVM projects working on real-time proving have leveraged server-side GPUs (e.g. CUDA on RTX-5090) for ~79x improvement on average proving times, according to site metrics from Jan 28, 2025 to Jan 23, 2026, validating the potential of GPU acceleration for proving.

On the client side, though still in the early stages of PoC and exploration, several projects highlight potential:

• Ingonyama ICICLE Metal: Optimizes ZK primitives such as MSM and NTT for Apple's Metal API, achieving up to 5x acceleration on iOS/macOS GPUs (v3.6 release detailed in their blog post).
• zkMopro Metal MSM v2: Explores MSM acceleration on Apple GPUs, improved 40-100x over v1. For details, check this write-up. Building on ZPrize 2023 winners Tal and Koh's WebGPU innovations (inspired by their implementation) ⁶.
• Ligetron: Leverages WebGPU for faster SHA-256 and NTT operations, enabling cross-platform ZK both natively and in browsers.

Broader efforts from ZPrize and Geometry.xyz underscore growing momentum, though protocol integration remains limited ⁷⁸.

Opportunities for Acceleration​

Several ZK primitives are inherently parallelizable, making GPUs a natural fit:

• MSM (Multi-Scalar Multiplication): Sums scalar multiplications on elliptic curves; parallel via independent additions, bottleneck in elliptic curve-related schemes.
• NTT (Number Theoretic Transform): A fast algorithm for polynomial multiplication similar to FFT but over finite fields; parallel via butterfly ops, core to polynomial operations in many schemes.
• Polynomial Evaluation and Matrix-Vector Multiplication: Computes polynomial values at points or matrix-vector products; high-throughput on GPU shaders via SIMD parallelism.
• Merkle Tree Commitments: Builds hashed tree structures for efficient verification; parallel-friendly for batch processing and hashing.

Additionally, building blocks in interactive oracle proofs (IOPs), such as the sumcheck protocol ⁹, which reduces multivariate polynomial sums to univariate checks, benefit from massive parallelism in tasks such as summing large datasets or verifying constraints. While promising for GPU acceleration in schemes like WHIR ¹⁰ or GKR-based systems ¹¹, sumcheck is not currently the primary bottleneck in most polynomial commitment schemes (PCS).

These primitives map directly to bottlenecks in popular PCS, as shown in the table below.

PCS Type	Typical Schemes	Family (Hardness Assumption)	Primary Prover Bottleneck	Acceleration Potential	PQ Secure
KZG 12	Groth16, PlonK, Libra	Pairing-based (-SDH)	MSM	Moderate: Memory-bandwidth limited	No
IPA 13	Halo2, Bulletproofs, Hyrax	Discrete Log (DL)	MSM	Moderate: Parallel EC additions	No
Hyrax 14	GKR-based SNARKs	Discrete Log (DL)	MSM	Moderate: Similar to IPA but multilinear	No
LaBRADOR 15	LaBRADOR-based SNARKs	Lattice-based (SIS / LWE)	NTT, Matrix-Vector Ops	High: Fast small-integer arithmetic	Yes
FRI 16 / STIR 17	STARKs, Plonky2	Hash-based (CRHF)	Hashing, NTT	High: Extremely parallel throughput	Yes
WHIR 10	Multivariate SNARKs	Hash-based (CRHF)	Hashing	High: Extremely parallel throughput	Yes
Basefold 18	Basefold-SNARKs	Hash-based (CRHF)	Linear Encoding & Hashing	High: Field-agnostic parallel encoding	Yes
Brakedown 19	Binius, Orion	Hash-based (CRHF)	Linear Encoding	High: Bit-slicing (SIMD)	Yes

Table 1: ZK primitives mapped to PCS bottlenecks and GPU potential

Moreover, VOLE-based ZK proving systems, such as QuickSilver ²⁰, Wolverine ²¹, and Mac'n'Cheese ²², utilize vector oblivious linear evaluation (VOLE) to construct efficient homomorphic commitments. These act as PCS based on symmetric cryptography or learning parity with noise (LPN) assumptions. The systems are post-quantum secure. Their main prover bottlenecks are VOLE extensions, hashing, and linear operations, which make them well-suited for GPU acceleration through parallel correlation generation and batch processing.

In the short term, primitives related to ECC (e.g. MSM in pairing-based schemes) are suitable for accelerating existing, well-adopted proving systems like Groth16 or those using KZG commitments, providing immediate performance gains for current Ethereum applications.

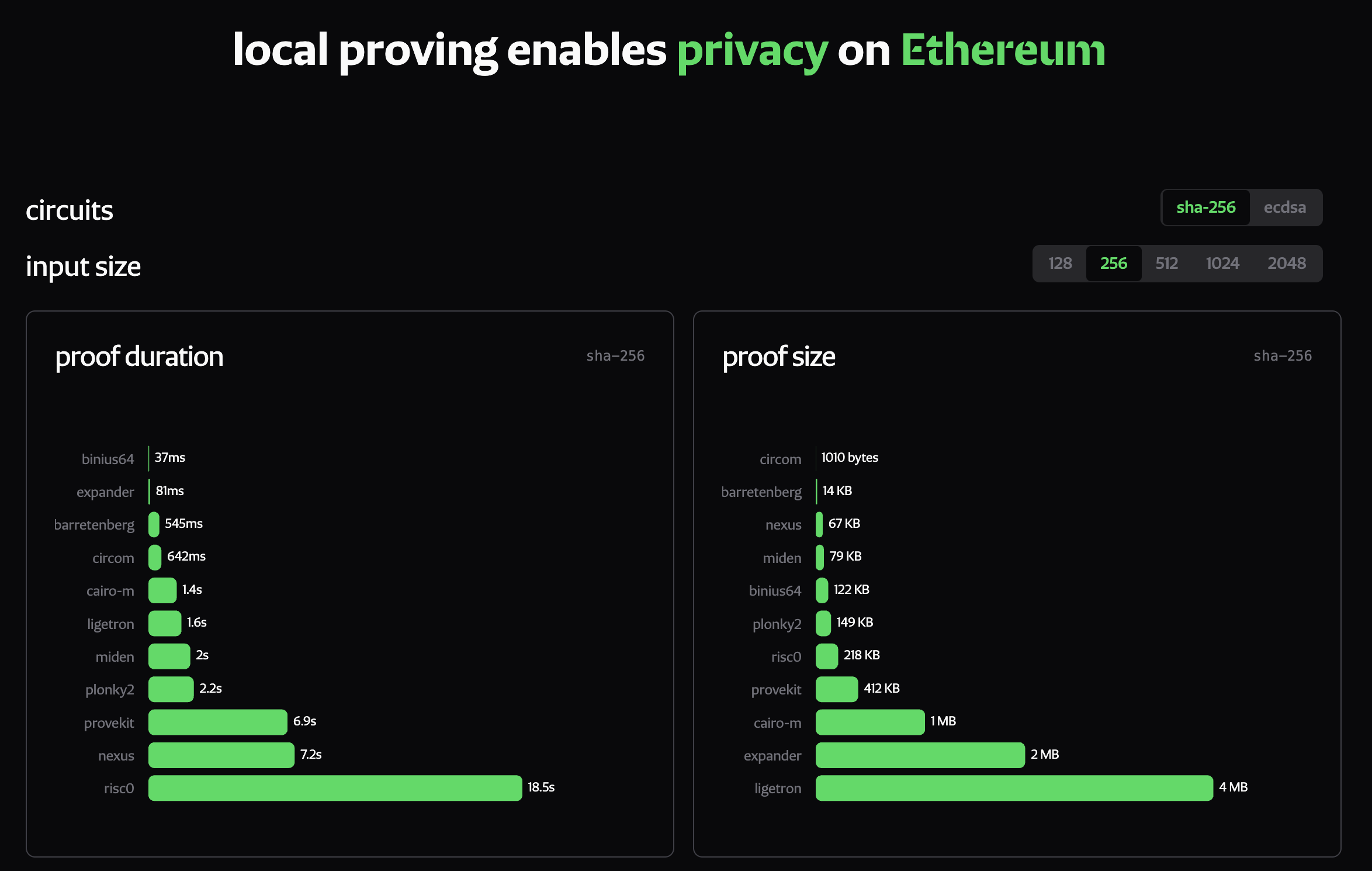
Quantum preparedness adds urgency for the long term: schemes on smaller fields (e.g. 31-bit fields like Mersenne 31, Baby Bear, or Koala Bear ²³) align better with GPU native words (32-bit), yielding higher throughput. Field-Ops Benchmarks ⁴ confirm this. Under the same settings (not optimal for max performance but for fairness of experiment), smaller fields like M31 achieve over 100 Gops/s on client GPUs, compared to <1 Gops/s for larger ones like BN254.

Operation	Metal GOP/s	WebGPU GOP/s	Ratio
u32_add	264.2	250.1	1.06x
u64_add	177.5	141.1	1.26x
m31_field_add	146.0	121.7	1.20x
m31_field_mul	112.0	57.9	1.93x
bn254_field_add	7.9	1.0	7.64x
bn254_field_mul	0.63	0.08	7.59x

As quantum tech advances, exploration related to PQ primitives (e.g. lattice-based or hash-based operations) will drive mid-to-long-term client-side proving advancements, ensuring resilience against quantum threats like "Harvest Now, Decrypt Later" (HNDL) attacks, as mentioned in the Federal Reserve HNDL Paper and underscored by the Ethereum Foundation's long-term quantum strategy, which is a critical factor if we are going to defend people's privacy on a daily-life scale.

3. Challenges: Bridging the Gap to Everyday Privacy​

Despite progress, some hurdles remain between the current status and everyday usability.

3.1 Fragmented Implementation​

• No standard crypto library exists for client-side GPUs, forcing developers to reinvent wheels from scratch, which is often not fully optimized.
• Lack of State-of-the-Art (SoTA) references for new explorations, leading to duplicated efforts.
• Inconsistent benchmarking: metrics like performance, I/O overhead, peak memory, and thermal/power traces are rarely standardized, complicating comparisons. Luckily, PSE's client-side proving team is improving this ⁵.

3.2 Limited Quantum-Resistant Support​

Most GPU accelerations have focused on PCS related to elliptic-curve cryptography (ECC) like IPA, Hyrax, and KZG (pairing-based). All are vulnerable to quantum attacks via Shor's algorithm. These operate on larger fields (e.g. 254-bit), inefficient for GPUs' 32-bit native operations, and schemes like Groth16 face theoretical acceleration upper bounds, as analyzed in Ingonyama's blog post on hardware acceleration for ZKP ²⁴. On the other hand, PQ schemes such as those based on lattices or hashes (e.g. FRI variants) are underexplored on client GPUs but offer greater parallelism.

3.3 Device-Specific Constraints​

Client devices differ vastly from servers: limited resources, shared GPU duties (e.g. graphics rendering), and thermal risks. Blindly offloading to GPUs can cause crashes or battery drain ^{25 26}. Hybrid CPU-GPU approaches, inspired by Vitalik's Glue and Coprocessor architecture, need further exploration. Key unknowns include:

• Task dispatching hyperparameters.
• Caching in unified memory. Check Ingonyama's Metal PoC for zero-cost CPU-GPU transfers.
• Balancing operations: GPUs for parallelism, CPUs for sequential tasks.

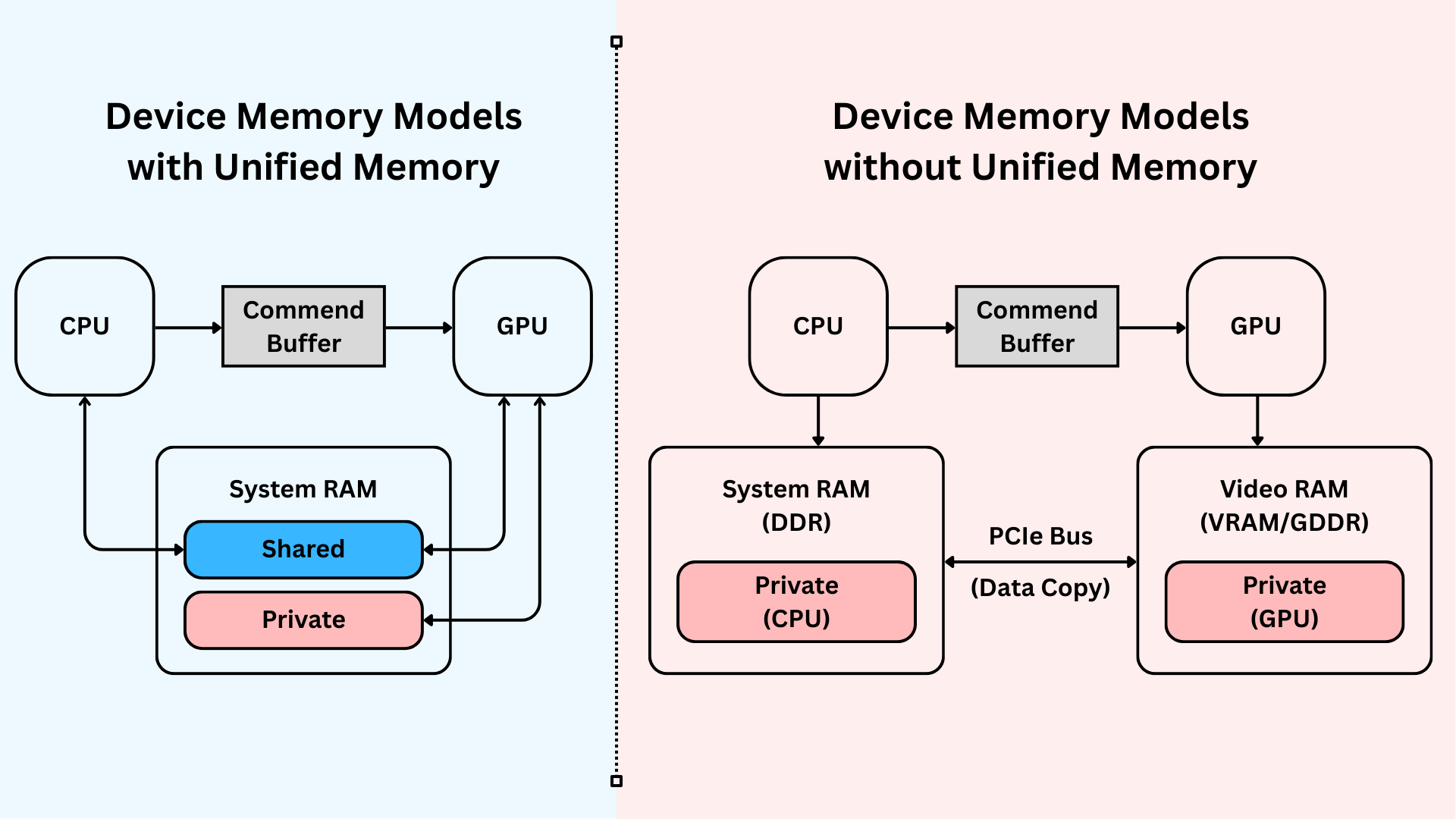Apple GPUs have the unified memory model in which the CPU and the GPU share system memory

4. PSE's Roadmap for GPU Acceleration​

To achieve client-side GPU acceleration's full potential, we propose a structured roadmap focused on collaboration and sustainability:

1. Build Standard Cryptography GPU Libraries for ZK

   • Mirror Arkworks's success in Rust zkSNARKs: Create modular, reusable libs optimized for client GPUs (e.g. low RAM, sustained performance) ²⁷.
   • Prioritize PQ foundations to enable HNDL-resistant solutions. For example, lattice-based primitives like NTT that scale with GPU parallelism ²⁸.
   • Make it community-owned, involving Ethereum, ZK, and privacy ecosystems for joint development, accelerating iteration and adoption in projects like mobile digital wallets.

2. Develop Best-Practice References

   • Integrate GPU acceleration into client-side suitable protocols, including at least one PQ scheme and mainstream ones like Plonky3 ²⁹ or Jolt ³⁰.
   • Optimize for mobile, tuning for sustained performance over peaks and avoiding thermal throttling via hybrid CPU-GPU coordination.
   • Create demo protocols as end-to-end references running on real devices with GPU boosts, serving as "how-to" guides for adopting standard libs.

This path transitions from siloed projects to ecosystem-wide tools, paving the way for explorations in sections like our starting points below.

5. Starting Points​

zkSecurity's WebGPU overview highlights its constraints versus native APIs like Metal or Vulkan. For example, limited integer support and abstraction overheads.

To validate, a PoC was conducted to compare field operations (M31 vs. BN254) across APIs ⁴. Key findings:

• u64 Emulation Overhead: Metal's native 64-bit support edges WebGPU (1.26x slower due to u32 emulation), compounding on complex ops.
• Field Size vs. Throughput: Smaller fields shine. M31 hits 100+ Gops/s; BN254 <1 Gops/s (favoring PQ schemes).
• Complexity Amplifies Gaps: Simple u32 ops show parity (1.06x); advanced arithmetic like Montgomery multiplication widens to 7x for BN254.

Start with native APIs first, such as Metal for iOS (sustainable boosts), then WebGPU for cross-platform reach. This prioritizes real-world viability over premature optimization.

6. Conclusion​

Client-side GPU acceleration for ZKPs represents both immediate and long-term opportunities for Ethereum privacy, potentially improving UX for adopting privacy-preserving tech and enabling quantum-secure daily-life use cases like private payments. By addressing fragmentation, embracing PQ schemes, and optimizing for mobile devices, we can make privacy "hygiene" for everyone (from casual users to privacy-maximalists). We believe that with collaborative efforts from existing players and the broader community, everyday Ethereum privacy is within reach.

Footnotes​

1. Kasra Abbaszadeh, Hossein Hafezi, Jonathan Katz, & Sarah Meiklejohn. (2025). Single-Server Private Outsourcing of zk-SNARKs. Cryptology ePrint Archive. https://eprint.iacr.org/2025/2113 ↩ ↩²

2. Takamichi Tsutsumi. (2025). TEE based private proof delegation. https://pse.dev/blog/tee-based-ppd ↩

3. Takamichi Tsutsumi. (2025). Constant-Depth NTT for FHE-Based Private Proof Delegation. https://pse.dev/blog/const-depth-ntt-for-fhe-based-ppd ↩

4. Field-Ops Benchmarks. GitHub. https://github.com/moven0831/field-ops-benchmarks ↩ ↩² ↩³

5. Proving Backends Benchmarks by Client-side Proving Team from PSE. https://ethproofs.org/csp-benchmarks ↩ ↩²

6. ZPrize 2023 Entry: Tal and Koh's WebGPU MSM Implementation. GitHub. https://github.com/z-prize/2023-entries/tree/main/prize-2-msm-wasm/webgpu-only/tal-derei-koh-wei-jie ↩

7. ZPrize. (2023). Announcing the 2023 ZPrize Winners. https://www.zprize.io/blog/announcing-the-2023-zprize-winners ↩

8. Geometry: Curve Arithmetic Implementation in Metal. GitHub. https://github.com/geometryxyz/msl-secp256k1 ↩

9. Carsten Lund, Lance Fortnow, Howard Karloff, & Noam Nisan. (1992). Algebraic methods for interactive proof systems. Journal of the ACM (JACM). https://dl.acm.org/doi/10.1145/146585.146605 ↩

10. Gal Arnon, Alessandro Chiesa, Giacomo Fenzi, & Eylon Yogev. (2024). WHIR: Reed–Solomon Proximity Testing with Super-Fast Verification. Cryptology ePrint Archive. https://eprint.iacr.org/2024/1586 ↩ ↩²

11. Shafi Goldwasser, Yael Tauman Kalai, & Guy N. Rothblum. (2008). Delegating computation: interactive proofs for muggles. In Proceedings of the fortieth annual ACM symposium on Theory of computing. https://dl.acm.org/doi/10.1145/1374376.1374396 ↩

12. Aniket Kate, Gregory M. Zaverucha, & Ian Goldberg. (2010). Constant-Size Commitments to Polynomials and Their Applications. In Advances in Cryptology - ASIACRYPT 2010. Springer. https://link.springer.com/chapter/10.1007/978-3-642-17373-8_11 ↩

13. Jonathan Bootle, Andrea Cerulli, Pyrros Chaidos, Jens Groth, & Christophe Petit. (2016). Efficient Zero-Knowledge Arguments for Arithmetic Circuits in the Discrete Log Setting. Cryptology ePrint Archive. https://eprint.iacr.org/2016/263 ↩

14. Riad S. Wahby, Ioanna Tzialla, abhi shelat, Justin Thaler, & Michael Walfish. (2017). Doubly-efficient zkSNARKs without trusted setup. Cryptology ePrint Archive. https://eprint.iacr.org/2017/1132 ↩

15. Ward Beullens & Gregor Seiler. (2022). LaBRADOR: Compact Proofs for R1CS from Module-SIS. Cryptology ePrint Archive. https://eprint.iacr.org/2022/1341 ↩

16. Eli Ben-Sasson, Iddo Bentov, Yinon Horesh, & Michael Riabzev. (2018). Scalable, transparent, and post-quantum secure computational integrity. Cryptology ePrint Archive. https://eprint.iacr.org/2018/046 ↩

17. Gal Arnon, Alessandro Chiesa, Giacomo Fenzi, & Eylon Yogev. (2024). STIR: Reed–Solomon Proximity Testing with Fewer Queries. Cryptology ePrint Archive. https://eprint.iacr.org/2024/390 ↩

18. Hadas Zeilberger, Binyi Chen, & Ben Fisch. (2023). BaseFold: Efficient Field-Agnostic Polynomial Commitment Schemes from Foldable Codes. Cryptology ePrint Archive. https://eprint.iacr.org/2023/1705 ↩

19. Alexander Golovnev, Jonathan Lee, Srinath Setty, Justin Thaler, & Riad S. Wahby. (2021). Brakedown: Linear-time and field-agnostic SNARKs for R1CS. Cryptology ePrint Archive. https://eprint.iacr.org/2021/1043 ↩

20. Kang Yang, Pratik Sarkar, Chenkai Weng, & Xiao Wang. (2021). QuickSilver: Efficient and Affordable Zero-Knowledge Proofs for Circuits and Polynomials over Any Field. Cryptology ePrint Archive. https://eprint.iacr.org/2021/076 ↩

21. Chenkai Weng, Kang Yang, Jonathan Katz, & Xiao Wang. (2020). Wolverine: Fast, Scalable, and Communication-Efficient Zero-Knowledge Proofs for Boolean and Arithmetic Circuits. Cryptology ePrint Archive. https://eprint.iacr.org/2020/925 ↩

22. Carsten Baum, Alex J. Malozemoff, Marc B. Rosen, & Peter Scholl. (2020). Mac'n'Cheese: Zero-Knowledge Proofs for Boolean and Arithmetic Circuits with Nested Disjunctions. Cryptology ePrint Archive. https://eprint.iacr.org/2020/1410 ↩

23. Voidkai. Efficient Prime Fields for Zero-knowledge proof. HackMD. https://hackmd.io/@Voidkai/BkNX3xUZA ↩

24. Ingonyama. (2023, September 27). Revisiting Paradigm’s “Hardware Acceleration for Zero Knowledge Proofs”. Medium. https://medium.com/@ingonyama/revisiting-paradigms-hardware-acceleration-for-zero-knowledge-proofs-5dffacdc24b4 ↩

25. "GPU in Your Pockets", zkID Days Talk at Devconnect 2025. https://streameth.org/6918e24caaaed07b949bbdd1/playlists/69446a85e505fdb0fa31a760 ↩

26. Benoit-Cattin, T., Velasco-Montero, D., & Fernández-Berni, J. (2020). Impact of Thermal Throttling on Long-Term Visual Inference in a CPU-Based Edge Device. Electronics, 9(12), 2106. https://doi.org/10.3390/electronics9122106 ↩

27. Arkworks. https://arkworks.rs/ ↩

28. Jillian Mascelli & Megan Rodden. (2025, September). “Harvest Now Decrypt Later”: Examining Post-Quantum Cryptography and the Data Privacy Risks for Distributed Ledger Networks. Federal Reserve Board. https://www.federalreserve.gov/econres/feds/files/2025093pap.pdf ↩

29. Plonky3. GitHub. https://github.com/Plonky3/Plonky3 ↩

30. Jolt. GitHub. https://github.com/a16z/jolt ↩

Key Takeaways​

• Hybrid CPU-GPU approaches are essential for fully exploiting limited hardware such as mobile devices, improving MSM computation and accelerating proof generation.
• To unify GPU acceleration efforts, WebGPU's vendor-agnostic API and WGSL offer promising solutions that compile to native formats like SPIR-V (for Vulkan on Android) and MSL (for Metal on Apple devices).
• GPU acceleration for post-quantum proving systems could enable their widespread adoption.

Introduction​

GPU acceleration harnesses the massive parallelism of Graphics Processing Units (GPUs) to dramatically speed up tasks that would otherwise overwhelm traditional CPUs. Because GPUs can execute thousands of threads simultaneously, they have become indispensable for compute-intensive workloads such as machine-learning model training and modern cryptographic algorithms.

This technology plays a crucial role in advancing privacy-preserving applications, as zero-knowledge proofs (ZKPs) currently face a significant bottleneck due to the high computational cost of their core operations. By accelerating these operations, we can generate proofs more quickly and cost-effectively, which is essential for the broader adoption of privacy-focused solutions across Ethereum and other blockchain platforms.

Currently, research on GPU acceleration for cryptography remains fragmented, with each platform relying on its own framework: Metal on Apple devices, Vulkan on Android, and CUDA on NVIDIA hardware. Aside from CUDA, most GPU frameworks lack mature ecosystems of cryptographic libraries (e.g., NVIDIA's cuPQC and cuFFT).

Therefore, Mopro is investing in GPU acceleration through related grants (Issue #21, Issue #22, and Issue #153), as it advances our mission to make mobile proving both accessible and practical.

A Primer on Multi-Scalar Multiplication​

Multi-Scalar Multiplication (MSM) is an essential primitive in elliptic curve cryptography, particularly in pairing-based proving systems widely used for privacy-preserving applications. MSM involves computing a sum of the form $Q = \sum_{i=1}^{n}(k_i \cdot P_i)$, where $k_i$ are scalars and $P_i$ are points on an elliptic curve, such as BN254. This computationally intensive operation is ideal for GPU acceleration.

Metal MSM v2 is an open-source implementation, licensed under MIT and Apache 2.0, that optimizes MSM on Apple GPUs using the Metal Shading Language (MSL). Building on its predecessor, Metal MSM v2 offers significant performance improvements through algorithmic and GPU-specific optimizations, laying the foundation for further research into mobile proving acceleration with GPUs.

Recap on Metal MSM v1​

The first version of Metal MSM (v1) was an initial attempt to bring MSM computations on the BN254 curve to Apple GPUs, leveraging parallelism and optimizations like precomputation from the EdMSM paper by Bootle et al.¹. While it showed the potential for GPU acceleration, profiling result revealed key limitations:

• Low GPU Occupancy: At only 32%, the GPU was underutilized, leading to inefficient computation.
• High Memory Footprint: Peak VRAM usage was excessive, causing GPU hang errors on real mobile devices for instance sizes ≥ 2^14.
• Performance Bottlenecks: For an input size of 2^20 points, v1 took 41 seconds on an M1 Pro MacBook, indicating substantial room for improvement.

These challenges drove the development of a newer version, which introduces targeted optimizations to address these issues. For full context, refer to the detailed Metal MSM v1 Summary Report and Metal MSM v1 Profiling Report.

Metal MSM v2: What's New​

Metal MSM v2 introduces key enhancements over v1, significantly improving performance and resource efficiency. It adopts the sparse matrix approach from the cuZK paper by Lu et al.², treating MSM elements as sparse matrices to reduce memory usage and convert operations described in Pippenger's algorithm into efficient sparse matrix algorithms.

The implementation draws inspiration from Derei and Koh's WebGPU MSM implementation for ZPrize 2023. However, targeting the BN254 curve (unlike the BLS12-377 curve used by Zprize 2023) required different optimization strategies, particularly for Montgomery multiplications and for using Jacobian coordinates instead of projective or extended twisted Edwards coordinates.

Due to differences between shading languages (CUDA for cuZK, WGSL for WebGPU, and MSL for Metal), additional GPU programming efforts were necessary. For instance, dynamic kernel dispatching, which is straightforward in CUDA, required workarounds in Metal through host-side dispatching at runtime.

Key improvements include:

• Dynamic Workgroup Sizing: Workgroup sizes are adjusted based on input size and GPU architecture using a scale_factor and thread_execution_width. These parameters were optimized through experimentation to maximize GPU utilization as mentioned in PR #86.
• Dynamic Window Sizes: A window_size_optimizer calculates optimal window sizes using a cost function from the cuZK paper, with empirical adjustments for real devices, as detailed in PR #87.
• MSL-Level Optimizations: Loop unrolling and explicit access qualifiers, implemented in PR #88, enhance kernel efficiency, with potential for further gains via SIMD refactoring.

Benchmarks on an M3 MacBook Air with 24GB memory show 40x–100x improvements over v1 and ~10x improvement over ICME Labs' WebGPU MSM on BN254, adapted from Derei and Koh's BLS12-377 work. While still slower than CPU-only Arkworks MSM on small & medium input sizes, v2 lays the groundwork for a future CPU+GPU hybrid approach.

How Metal MSM v2 Works​

The general flow follows Koh's technical writeup. We pack affine points and scalars on the CPU into a locality-optimized byte format, upload them to the GPU, and encode points into Montgomery form for faster modular multiplications. Scalars are split into signed chunks to enable the Non-Adjacent Form (NAF) method, halving both bucket count and memory during accumulation.

Next, we apply a parallel sparse-matrix transposition (adapted from Wang et al.'s work³) to identify matching scalar chunks and group points into buckets. Then, using a sparse-matrix–vector product (SMVP) and the pBucketPointsReduction algorithm (Algorithm 4 in the cuZK paper²), we split buckets among GPU threads, compute each thread's running sum, and scale it by the required factor.

After GPU processing, we transfer each thread's partial sums back to the CPU for final aggregation. Since the remaining point count is small and Horner's Method is sequential and efficient on the CPU, we perform the final sum there.

The use of sparse matrices is a key innovation in Metal MSM v2, reducing memory requirements and boosting parallelism compared to previous approaches.

Understanding the Theoretical Acceleration Upper Bound​

In the Groth16 proving system, Number Theoretic Transform (NTT) and MSM account for 70–80% of the proving time. According to Amdahl's Law, the maximum speedup is limited by unoptimized components:

$\text{Speedup}_{\text{overall}} = \dfrac{1}{(1 - \text{time}_{\text{optimized}}) + \dfrac{\text{time}_{\text{optimized}}}{\text{speedup}_{\text{optimized}}}}$

If 80% of the prover time is optimized with infinite speedup, the theoretical maximum is 5x. However, data I/O overhead reduces practical gains. For more details, see Ingonyama's blog post on Hardware Acceleration for ZKP.

Benchmark Results​

Benchmarks conducted on an M3 MacBook Air compare Metal MSM v2 with the Arkworks v0.4.x CPU implementation across various input sizes.

Scheme	Input Size (ms)
	212	214	216	218	220	222	224
Arkworks v0.4.x (CPU, Baseline)	6	19	69	245	942	3,319	14,061
Metal MSM v0.1.0 (GPU)	143 (-23.8x)	273 (-14.4x)	1,730 (-25.1x)	10,277 (-41.9x)	41,019 (-43.5x)	555,877 (-167.5x)	N/A
Metal MSM v0.2.0 (GPU)	134 (-22.3x)	124 (-6.5x)	253 (-3.7x)	678 (-2.8x)	1,702 (-1.8x)	5,390 (-1.6x)	22,241 (-1.6x)
ICME WebGPU MSM (GPU)	N/A	N/A	2,719 (-39.4x)	5,418 (-22.1x)	17,475 (-18.6x)	N/A	N/A
ICICLE-Metal v3.8.0 (GPU)	59 (-9.8x)	54 (-2.8x)	89 (-1.3x)	149 (+1.6x)	421 (+2.2x)	1,288 (+2.6x)	4,945 (+2.8x)
ElusAegis' Metal MSM (GPU)	58 (-9.7x)	69 (-3.6x)	100 (-1.4x)	207 (+1.2x)	646 (+1.5x)	2,457 (+1.4x)	11,353 (+1.2x)
ElusAegis' Metal MSM (CPU+GPU)	13 (-2.2x)	19 (-1.0x)	53 (+1.3x)	126 (+1.9x)	436 (+2.2x)	1,636 (+2.0x)	9,199 (+1.5x)

Negative values indicate slower performance relative to the CPU baseline. The performance gap narrows for larger inputs.

Notes:

• For ICME WebGPU MSM, input size 2^12 causes M3 chip machines to crash; sizes not listed on the project's GitHub page are shown as "N/A"
• For Metal MSM v0.1.0, the 2^24 benchmark was abandoned due to excessive runtime.

While Metal MSM v2 isn't faster than CPUs across all hardware configurations, its open-source nature, competitive performance relative to other GPU implementations, and ongoing improvements position it well for continued advancement.

Profiling Insights​

Profiling on an M1 Pro MacBook provides detailed insights into the improvements from v1 to v2:

metric	v1	v2	gain
end-to-end latency	10.3 s	0.42 s	24x
GPU occupancy	32 %	76 %	+44 pp
CPU share	19 %	<3 %	–16 pp
peak VRAM	1.6 GB	220 MB	–7.3×

These metrics highlight the effectiveness of v2's optimizations:

• Latency Reduction: A 24-fold decrease in computation time for 2^20 inputs.
• Improved GPU Utilization: Occupancy increased from 32% to 76%, indicating better use of GPU resources.
• Reduced CPU Dependency: CPU share dropped below 3%, allowing the GPU to handle most of the workload.
• Lower Memory Footprint: Peak VRAM usage decreased from 1.6 GB to 220 MB, a 7.3-fold reduction.

Profiling also identified buffer reading throughput as a primary bottleneck in v1, which v2 mitigates through better workload distribution and sparse matrix techniques. See detailed profiling reports: v1 Profiling Report and v2 Profiling Report.

Comparison to Other Implementations​

Metal MSM v2 is tailored for Apple's Metal API, setting it apart from other GPU-accelerated MSM implementations:

• Derei and Koh's WebGPU MSM on BLS12: Designed for WebGPU, this implementation targets browser-based environments and may not fully leverage Apple-specific hardware optimizations.
• ICME labs WebGPU MSM on BN254: Adapted from Derei and Koh's WebGPU work for the BN254 curve, it is ~10x slower than Metal MSM v2 for inputs from 2^16 to 2^20 on M3 MacBook Air.
• cuZK: A CUDA-based implementation for NVIDIA GPUs, operating on a different hardware ecosystem and using different algorithmic approaches.

Metal MSM v2's use of sparse matrices and dynamic workgroup sizing provides advantages on Apple hardware, particularly for large input sizes. While direct benchmark comparisons are limited, internal reports suggest that v2 achieves performance on par with or better than other WebGPU/Metal MSM implementations at medium scales.

It's worth noting that the state-of-the-art Metal MSM implementation is Ingonyama's ICICLE-Metal (since ICICLE v3.6). Readers can try it by following:

• ICICLE Rust MSM example
• Experimental BN254 Metal benchmark

Another highlight is ElusAegis' Metal MSM implementation for BN254, which was forked from version 1 of Metal MSM. To the best of our knowledge, his pure GPU implementation further improves the allocation and algorithmic structure to add more parallelism, resulting in 2x faster performance compared to Metal MSM v2.

Moreover, by integrating this GPU implementation with optimized MSM on the CPU side from the halo2curves library, he developed a hybrid approach that splits MSM tasks between CPU and GPU and then aggregates the results. This strategy achieves an additional 30–40% speedup over a CPU-only implementation. This represents an encouraging result for GPU acceleration in pairing-based ZK systems and suggests a promising direction for Metal MSM v3.

Future Work​

The Metal MSM team has outlined several exciting directions for future development:

• SIMD Refactoring: Enhance SIMD utilization and memory coalescing to further boost performance.
• Advanced Hybrid Approach: Integrate with Arkworks 0.5 for a more sophisticated CPU-GPU hybrid strategy.
• Android Support: Port kernels to Vulkan compute/WebGPU on Android, targeting Qualcomm Adreno (e.g., Adreno 7xx series) and ARM Mali (e.g., G77/G78/G710) GPUs.
• Cross-Platform Support: Explore WebGPU compatibility to enable broader platform support.
• Dependency Updates: Transition to newer versions of objc2 and objc2-metal, and Metal 4 to leverage the latest MTLTensor features, enabling multi-dimensional data to be passed to the GPU.

Beyond these technical improvements, we are also interested in:

• Exploration of PQ proving schemes: With the limited acceleration achievable from pairing-based proving schemes, we're motivated to explore PQ-safe proving schemes that have strong adoption potential over the next 3–5 years. These schemes, such as lattice-based proofs, involve extensive linear algebra operations that can benefit from GPUs' parallel computing capabilities.
• Crypto Math Library for GPU: Develop comprehensive libraries for cryptographic computations across multiple GPU frameworks, including Metal, Vulkan, and WebGPU, to expand the project's overall scope and impact.

Conclusion​

Metal MSM v2 represents a leap forward in accelerating Multi-Scalar Multiplication on Apple GPUs. By addressing the limitations of v1 through sparse matrix techniques, dynamic thread management, and other novel optimization techniques, it achieves substantial performance gains for Apple M-series chips and iPhones.

However, two challenges remain:

• First, GPUs excel primarily with large input sizes (typically around 2^26 or larger). Most mobile proving scenarios use smaller circuit sizes, generally ranging from 2^16 to 2^20, which limits the GPU's ability to fully leverage its parallelism. Therefore, optimizing GPU performance for these smaller workloads remains a key area for improvement.
• Second, mobile GPUs inherently possess fewer cores and comparatively lower processing power than their desktop counterparts, constraining achievable performance. This hardware limitation necessitates further research into hybrid approaches and optimization techniques to maximize memory efficiency and power efficiency within the constraints of mobile devices.

Addressing these challenges will require ongoing algorithmic breakthroughs, hardware optimizations, and seamless CPU–GPU integration. Collectively, these efforts pave a clear path for future research and practical advancements that enable the mass adoption of privacy-preserving applications.

Get Involved​

We welcome researchers and developers interested in GPU acceleration, cryptographic computations, or programmable cryptography to join our efforts:

• GPU Exploration Repository (latest version includes Metal MSM v2)
• Mopro (Mobile Proving)

For further inquiries or collaborations, feel free to reach out through the project's GitHub discussions or directly via our Mopro community on Telegram.

Special Thanks​

We extend our sincere gratitude to Yaroslav Yashin, Artem Grigor, and Wei Jie Koh for reviewing this post and for their valuable contributions that made it all possible.

Footnotes​

1. Bootle, J., & Chiesa, A., & Hu, Y. (2022). "Gemini: elastic SNARKs for diverse environments." IACR Cryptology ePrint Archive, 2022/1400: https://eprint.iacr.org/2022/1400 ↩

2. Lu, Y., Wang, L., Yang, P., Jiang, W., Ma, Z. (2023). "cuZK: Accelerating Zero-Knowledge Proof with A Faster Parallel Multi-Scalar Multiplication Algorithm on GPUs." IACR Cryptology ePrint Archive, 2022/1321: https://eprint.iacr.org/2022/1321 ↩ ↩²

3. Wang, H., Liu, W., Hou, K., Feng, W. (2016). "Parallel Transposition of Sparse Data Structures." Proceedings of the 2016 International Conference on Supercomputing (ICS '16): https://synergy.cs.vt.edu/pubs/papers/wang-transposition-ics16.pdf ↩